What is mathematical formalism?
It is a set of equations that aims to represent in a non-ambiguous way an object of study and its temporal evolution in order to create a model. About twenty years ago, networks became popular in the modelling of complex systems for their ability to capture the interactions between parts of a system in a simple way with a universal formalism. If we think of social networks, we can think of people as the nodes of the network and their friendships as the edges of the network. But this formalism is much more general, as nodes can be airports and edges can be aeroplane connections, or molecules with their reactions. In many contexts, the information contained in the edges is not symmetrical, so we speak of directed edges and directed networks. To take the example of social networks, this would be similar to Twitter, where you can follow someone who does not necessarily follow you back. The comparison can also be made with the functioning of our brain in which the nodes are the neurons and the axons and dendrites are the edges, the flow of information between neurons often has a preferred direction.
As research continues to evolve, researchers have found that the network formalism fails to capture interactions that involve multiple bodies at the same time, a behaviour typical of a wide variety of phenomena. Think, for example, of how you behave with someone when you are in a pair. Do you act in the same way as when you are in a group? The reason for this limitation of networks is quite simple: in a network, an edge can only connect to two nodes, so there is no room for interactions with three or more. Moreover, quite often these multiple interactions have a preferred direction. For example, in the phenomena of peer pressure and bullying in sociology, these are group interactions but directed towards one or more people. In chemical reactions, several components must react together, but there is a preferred direction given by thermodynamics.
The idea developed by the Namur researchers with their Italian colleagues is to consider a formalism that takes into account both the multiple interactions and their direction. The UNamur research group was already studying asymmetric interactions, but in the framework of networks. On the other hand, the research group of the University of Catania had recently developed a formalism to deal with multiple but symmetric interactions. Their work entitled « Stability of synchronization in simplicial complexes » was published in Nature Communications.
Thanks to the collaboration between these two groups, the researchers were able to pool their skills and extend the Italian formalism to the Namur approach, making it possible to develop an even more general theory, including asymmetry in many-body interactions.
In this figure adapted from the article, we can consider the interaction between Huey, Dewey and Louie as the sum of the interaction of Huey and Dewey towards Louie, of Huey and Louie towards Dewey or even of Dewey and Louie towards Huey.
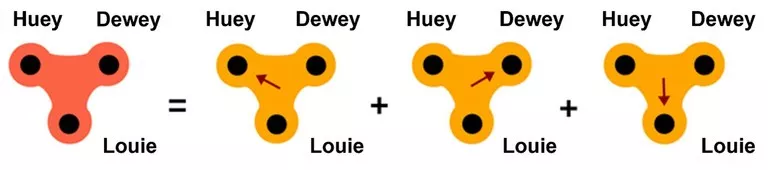
The new formalism made it possible to study the dynamics of the systems represented by these hypergraphs, which they called M-directed (where M is the number of nodes which receive the information, M=1 in the example in the figure), and extend classical results in this new context, opening the door to new and exciting future research. The theory can be used in different disciplines. From social sciences to epidemiological studies, there are many disciplines where there is experimental evidence of directed many-body interactions. From now on, researchers will be able to add one more tool to their toolbox to build more accurate models.
This collaboration was made possible thanks to the Erasmus+ program, which enabled Luca Gallo, doctoral student from the University of Catania and first author of the article, to stay at the UNamur for 9 months, and Riccardo Muolo, FNRS FRIA doctoral student at the UNamur and co-author of the article, to stay with the Catania group for two weeks. Supervised by Professor Carletti in Namur and by Professor Frasca in Catania, the two doctoral students were able to work together and learn the analytical and numerical techniques of the two research groups.
These results once again show the importance of collaborative projects in research, which promote the exchange of know-how and the emergence of new ideas.


The research teams
University of Catania (Italy)
- Prof Mattia Frasca
- Prof Vito Latora (also Queen Mary University - London)
- Dr Valentina Gambuzza
- Prof Luca Gallo
University of Namur (Belgium) - naXys Institute
- Prof Timoteo Carletti
- Riccardo Muolo (FNRS FRIA PhD student)